
这次来说说数组与链表。在说数组与链表之前,先来介绍一下线性表和非线性表。
线性表 LinearList
顾名思义,线性表的结构是线性的。就像图书馆书架上的书一样,每一行的书都是整齐的排列在直直的书板上。高楼在垂直方向上也可以说是线性的,每一层楼都可以看作是一个单位,依次上下排列。
说到线性表的本质,就是每个元素之间,只有前后关系。书架上的书,相邻的两本书,其中一本必然在另一本的前边或者后边(不考虑上下层)。相邻的两层楼,其中一层必然在另一层的上边或者下边。
由此看来,数组、链表都属于线性表,另外栈、队列也属于此类。
非线性表
与线性表对应的就是非线性表。非线性表的每个元素之间关系更加多元,不只是有前后关系。
一棵树,树干长出树枝,树枝又可以分叉,最后长出树叶。那树枝之间有父子关系、兄弟关系。一张地图,主要地点之间的关系则更加复杂。
数据结构中的树、图等都是非线性结构。
数组与链表
先来看一张图。

这是一个抽屉柜。但这也能够反应硬盘空间的结构。抽象来看,硬盘本质上就是一个一维的、每个元素相等大小紧密排列的结构,虽然硬盘我们看到是一个 3D 实物,但最终总能够映射成一维的空间。

数组则完全是硬盘结构的映射,使用连续的内存空间存储数据。可以说数组这种数据结构在使用内存上非常直接,申请一块连续的内存空间,然后存储数据即可。就好像 a、b、c 三人的房屋在一条街上各自相邻,去完 a 家,往右走两步就是 b 家,再走两步就是 c 家。
但是这也带来了一个核心问题——如果内存中没有一块连续的内存空间可供使用怎么办。在内存中我们运行着操作系统和众多软件。软件运行会加载到内存中,结束时会释放掉。经过反复的这个过程,我们的内存空间会变得十分零碎。很可能空余的空间有 100 个空位,但是这 100 个空位是不连续的、被其他正在使用中的内存分割开的,那我们申请 100 个空间的数组时也会失败。
这也导致了链表的产生。
链表为了解决数组强制要求分配连续空间的问题,通过在当前元素中记录下一个元素地址的方式,将多个分散在内存空间中的元素联系起来。就好像 a、b、c 三人的房屋并不是相连,而是隔了很远,但是 a 知道 b 家的地址,b 又知道 c 家的地址,这样我们只要知道 a 的地址,总能找到 b、c 的位置。
天下没有免费的午餐,链表虽然不需要连续的内存空间,但是每个元素需要记忆下一个元素的位置,这增加了链表单个元素的空间占用。相当于链表通过单个元素的空间占用来解绑整体内存空间连续的强制要求。算法与数据结构中充满了这种 Trade-Off。
总结一下,数组要求内存空间连续,但是只要通过简单的 base_address + k * size 的方式,就能够马上访问第 k 个元素,即具有 O(1) 随机访问的能力。链表不要求内存空间连续,但是需要从头开始,一个个依次访问元素之后才能够找到第 k 个元素。
对比
不管是数组还是链表,我们对其进行操作一般包括:插入数据、删除数据、查找数据。接下来我们通过这三个操作来对比一下两者。而分析的时候必然会涉及到时间复杂度,我们先来简单说说时间复杂度如何分析。
时间复杂度
我们一般会使用大 O 表示法来作为时间复杂度分析的工具,或者说表示方式。我们在进行时间复杂度分析时,并不关注算法的实际执行时间,而是关注代码执行时间在数据规模增长时的变化趋势。简单来说,我们分析的是在数据规模 n 下,代码的执行次数。最后用大 O 表示法表示。 结合如下伪代码,介绍一下其分析方法:
- 只关注循环执行次数最多的代码,忽略其常量、低阶、系数;
- 加法法则:一段代码的总复杂度,等于量级最大的那段代码的复杂度;
- 乘法法则:嵌套代码的复杂度等于内外代码复杂度的乘积。
complexity(int n) {
int[] array = new int[n];
// 1: O(1)
int a = array[0];
int b = array[1];
// 2: O(n)
for (int i = 0; i < n; i++) {
print(array[i]);
print(array[i]);
}
// 3: o(n^2)
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
print(array[i] * array[j]);
}
}
}
这里我们的数据量为 n。
首先我们看注释 1 处,虽然这里访问了两次 array,但是我们忽略其常量,所以这段代码复杂度为 O(1)。
我们再看注释 2 处,这里通过循环对数组进行打印了两次,访问了数组的所有元素,所以其代码复杂度为 O(2n),但是我们会忽略系数,所以这段代码时间复杂度为 O(n)。
我们最后看注释 3 处,通过两层循环嵌套,每个循环均访问了数据所有元素,打印数组元素的乘积,每层循环的时间复杂度为 O(n),根据乘法法则,这段代码的时间复杂度为 O(n) * O(n),即 O(n^2)。
那整体来看,这个函数的时间复杂度是多少呢?根据加法法则,同时我们会忽略低阶、常量的时间复杂度,最终我们的时间复杂度为 O(n^2)。
空间复杂度的分析方式和时间复杂度类似,只不过是把代码执行次数换成空间占用。
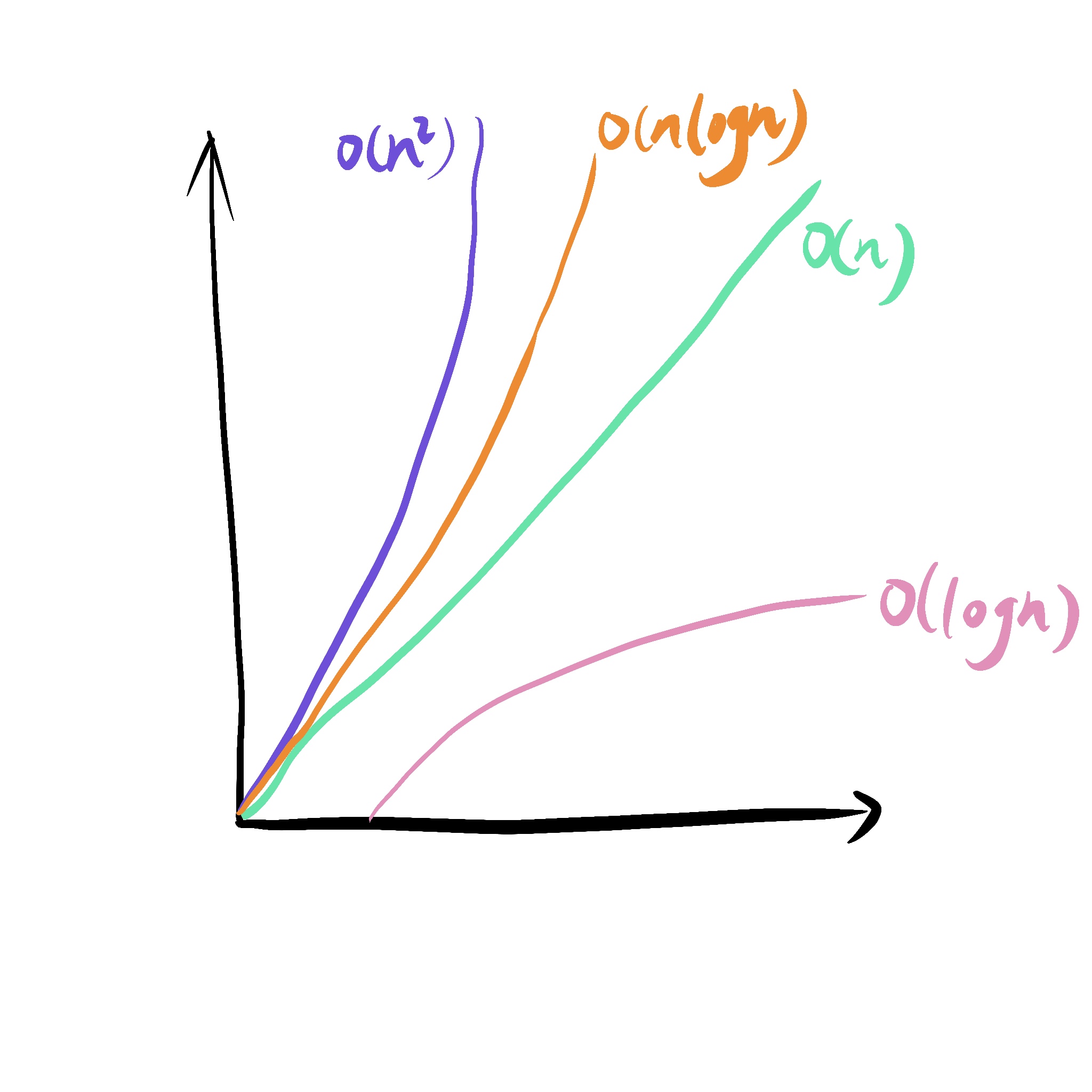
常见的时间复杂度有:O(1)、O(logn)、O(n)、O(nlogn)、O(n^2)、O(n!)。
接下来我们继续对比数组和链表。
插入数据
数组的插入数据分为两种,一种是有序数组插入后仍要保持数组元素有序,另一种是无序数组插入数据。先来看看第一种,为了保证数组的有序,所以我们需要将插入位置之后的数据往后搬移位置,最优情况是插入数组尾部,无需搬移数据,时间复杂度为 O(1),最坏的情况是插入头部,需要搬移所有的数据,时间复杂度为 O(n)。平均下来时间复杂度为 O(n),其平均时间复杂度可以通过权重的方式计算,在此不再详述。对于第二种无需数组则比较简单,假如我们插入的位置为 k,只需将第 k 个元素移到尾部,然后插入数据即可,时间复杂度为 O(1)。
链表的插入就比较简单,直接操作一下元素的指针指向即可,在 O(1) 时间复杂度即可完成。当然这里说的是已经知道插入位置的情况,不包含查找插入位置的过程。
删除数据
数组删除数据时,为了保证占用空间的连续,删除后需要搬移后续数据,所以其时间复杂度为 O(n)。当然这里可以做一下优化,即删除数据后不要马上搬移数据,而是先记录下来,空间不够时再进行一次搬移数据的操作。这个就是 Java 虚拟机垃圾回收机制中 标记清除算法 的核心思想。
链表删除数据也比较简单,直接操作元素的指针指向即可,时间复杂度为 O(1)。
访问数据
假设我们现在要访问第 k 个元素,数组因为空间连续的特性,通过上述地址计算公式直接拿到第 k 个元素的地址,直接访问即可,时间复杂度为 O(1)。链表则比较麻烦,因为其空间不连续,我们需要从头开始,一个一个的依次拿到后续元素的地址,直到第 k 个。所以其时间复杂度为 O(n)。
综上所述,我们可以得到下表。
| 数组 | 链表 | |
|---|---|---|
| 随机读取 | O(1) | O(n) |
| 插入 | O(n) | O(1) |
| 删除 | O(n) | O(1) |
总结
最后我们可以得出结论,数组与链表的主要区别在于内存空间是否连续。数组要求内存空间连续,所以分配内存时条件更加苛刻,但是这让数组能够 O(1) 随机访问元素。链表无需内存空间连续,分配内存的条件比较宽松,但是这导致链表占用空间更大,访问元素时间复杂度较高。
最后推荐一下我正在编写的小程序 VirtualLearning,它能够可视化一些算法与数据结构,让你更直观的学习。目前支持了主要的排序算法,更多内容扩充中,敬请期待。
微信扫码即可体验,或者搜索 VirtualLearning。
